速盈注册
Matlab全局优化算法——GA遗传算法
发布时间:2024-05-20 19:48:19 浏览次数:
前不久有小伙伴私信问我想学matlab需要去做些什么,跟他聊了很多给了他一些学习方面的建议!由此,我发现有很多小伙伴想要学习matlab但是苦于找不着门路,一些简单的算法的概念也不清晰!借此,我重新梳理一下一些算法,从简单的开始逐层递进,先讲解算法原理,再用matlab简单实现,不仅自己重新复习一下,同时也希望在matlab学习道路上能帮助到大家!
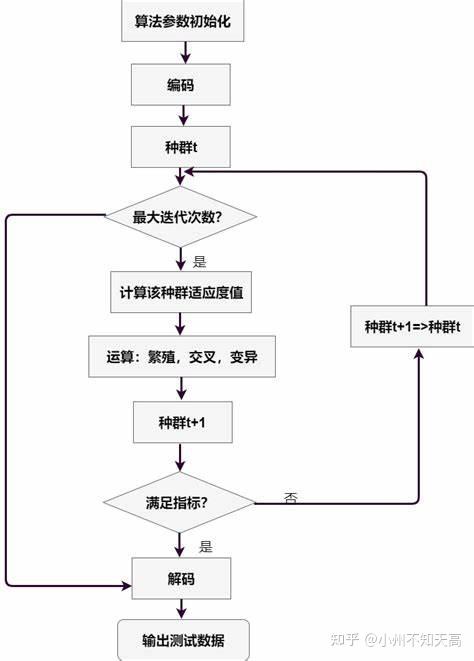
遗传算法(GA)是一种基于自然选择和基因遗传学原理,借鉴了生物进化优胜劣汰的自然选择机理和生物界繁衍进化的基因重组、突变的遗传机制的全局自适应概率搜索算法。
遗传算法是从一组随机产生的初始解(初始种群)开始的,这个种群由经过基因编码的一定数量的个体组成,每个个体实际上是染色体带有特征的实体。染色体作为遗传物质的载体,其内部表现(基因型)是某种基因组合,它决定了个体的外部表现。因此,从一开始就需要实现从表现型到基因型的映射,即编码工作。初始种群产生后,按照优胜劣汰的原理。逐代演化产生出越来越好的近似解。在每一代,根据问题域中的个体适应度大小选择个体,并借助于自然遗传学的遗传算子进行组合交叉和变异,产生出代表新的解集的种群。这个过程将导致种群像自然进化一样,后代种群比前代更加适应环境,末代种群中的最优个体,经过解码,可作为问题的近似最优解。
%遗传算法GA
%m函数文件 作用:初始化编码
%参数说明
%popsize :种群大小
%chromlength :染色体的长度
%作于2023-10-26 10:53:52 作者:Z
function pop = initpop(popsize,chromlength)
pop = round(rand(popsize,chromlength));
%round取整
end
其实,编码的过程就是10进制的值转为2进制!!!
%遗传算法GA
%m函数文件 作用:将二进制编码转化为十进制数
%参数说明
%pop :初始种群
%pop2 :解码后 转化成十进制后的种群
%作于 2023-10-26 10:59:55 作者:Z
function pop2 = decodebinary(pop)
[~,py] = size(pop);
for i = 1:py
pop1(:,i) = 2.^(py-i).*pop(:,i);
end
pop2 = sum(pop1,2);%遗传算法GA
%m函数文件 作用:计算目标函数值
%参数说明
%pop :初始种群
%temp1 :解码后十进制的值域数
%x :转换成变量域的数
%需要修改的参数:
%objvalue :目标函数
%作于 2023-10-26 11:12:51 作者:Z
function[objvalue]=calobjvalue(pop)
temp1=decodebinary(pop);
x=temp1.*10https://zhuanlan.zhihu.com/p/1023; %将二进制值域中的数转化为变量域中的数
%%计算目标函数值
objvalue=10*sin(5*x)+7*cos(4*x);这个比较重要,需要多加说明!!!
一般情况下,目标函数值已经能反映结果的好坏程度,比如说我们想求最值问题,目标函数的数值大小就已经能作为我们解决问题的评判条件了。
但是,当问题转变为最优解不取首尾两端,而在中间一段的时候,就不适合当评判标准了!
比如说,我们想求某化学实验的最佳温度,温度太高或者太低都不是我们的最佳解,所以我们需要用适应度函数对目标函数做一个变换(线性变换或者非线性变换),来使适应度能够胜任充当评委的工作!
ps:同时还要考虑目标函数值域落在正区间。
变换方法:
①对于最小化问题
②对于最大化问题
其中,F(x)为适应度函数,f(x)为目标函数
%遗传算法GA
%m函数文件 作用:计算个体的适应度值
%参数说明
%objvalue :目标函数值
%
%作于 2023-10-26 11:19:40 作者:Z
function fitvalue = calfitvalue(objvalue)
global Cmin;
Cmin = 0;
[px,~] = size(objvalue);
for i = 1:px
if objvalue(i)+Cmin > 0
temp = Cmin+objvalue(i);
else
temp = 0.0;
end
fitvalue(i) = temp;
end
fitvalue = fitvalue';①选择(复制)(Selection)
常见的选择方法有轮盘赌法、排序选择法、两两竞争法(又称锦标赛选择法)
这里详细介绍一下轮盘赌法:
轮盘赌法五步曲:
(1)、计算各染色体的 适应度
;
(2)、计算种群中所有染色体的适应值的和:
(3)、计算各染色体 的选择概率
:
(4)、计算各染色体 的累计概率
:
(5)、在[0,1]区间上内产生一个均匀分布的伪随机数 ,若
,则选择第一个染色体
;否则,选择第
个染色体,使得
成立。
%遗传算法GA
%m函数文件 作用 选择、复制
%本程序采用的是轮盘赌法
%参数说明
%pop :初始种群
%fitvalue :适应度值
%ms :升序排列的个体被选择概率 P(i)=ms(i+1)-ms(i);
%fitin :原种群个体的序列号 index1
%newin :新种群个体的序列号 index2
%newpop :新种群
%作于 2023-10-26 11:35:14 作者:Z
function [newpop]= selection2(pop,fitvalue)
totalfit = sum(fitvalue);%求适应度之和
fitvalue = fitvaluehttps://zhuanlan.zhihu.com/p/totalfit;%单个个体被选择的概率
fitvalue = cumsum(fitvalue);%累加函数
[px,~] = size(pop);
ms = sort(rand(px,1));%从小到大排列
fitin = 1;
newin = 1;
newpop = zeros(px,1);
while newin <= px
if(ms(newin)) <fitvalue(fitin)
newpop(newin) = pop(fitin);
newin = newin+1;
else
fitin = fitin+1;
end
end②.交叉操作(Crossover)
主要有单点交叉、两点交叉、多点交叉、均匀交叉等
%遗传算法GA
%m函数文件 作用 :交叉
%本程序采用的是(两点交叉)
%参数说明
%pop :初始种群
%pc :crossover的概率
%cpoint :crossover发生基因位点
%newpop :新种群
%作于 2023-10-26 11:35:14 作者:Z
function [newpop]= crossover2(pop,pc)
[px,py] = size(pop);
newpop = ones(size(pop));
for i = 1:2:px-1
if(rand < pc)
cpoint = round(rand*py);
newpop(i,:) = [pop(i,1:cpoint),pop(i+1,cpoint+1:py)];
newpop(i+1,:) = [pop(i+1,1:cpoint),pop(i,cpoint+1:py)];
else
newpop(i,:) = pop(i);
newpop(i+1,:) = pop(i+1);
end
end
③. 变异操作(Mutation)
变异操作的方法主要有基本位变异、均匀变异、边界变异、非均匀变异等.
这里需要注意的一点是:在生物学上相较于基因交换、和基因交叉,基因变异的概率是极小的!
所以我们的变异率不能设的太高!不然就成了随机搜索!
%遗传算法GA
%m函数文件 作用 :变异
%本程序采用的是基本位变异
%参数说明
%pop :初始种群
%pm :mutation发生的概率 pm不易过大!!
%mpoint :mutation 发生的基因点
%newpop :新种群
%作于 2023-10-26 11:48:19 作者:Z
function [newpop]= mutation2(pop,pm)
[px,py] = size(pop);
newpop = ones(size(pop));
for i = 1:px
if(rand < pm)
mpoint = round(rand*py);
if mpoint <= 0
mpoint = 1;
end
newpop(i) = pop(i);
%基因突变过程实现
if any(newpop(i,mpoint)) == 0
newpop(i,mpoint) = 1;
else
newpop(i,mpoint) = 0;
end
else %没有mutation
newpop(i) = pop(i);
end
end
遗传算法的终止条件有两个,满足任何一个条件,搜索就结束了。
① 连续多次前后两代群体的适应度变化小于阙值
即
② 达到了最大迭代次数(种群进化代数)
有了这些m函数文件作为基础,后面想要实现遗传算法就显得轻而易举了!!!
我们来用遗传算法求一下 y=10*sin(5*x)+7*cos(4*x) 这个函数最大值的一个优化问题!
这是itearation(迭代次数)为200时的一个结果:
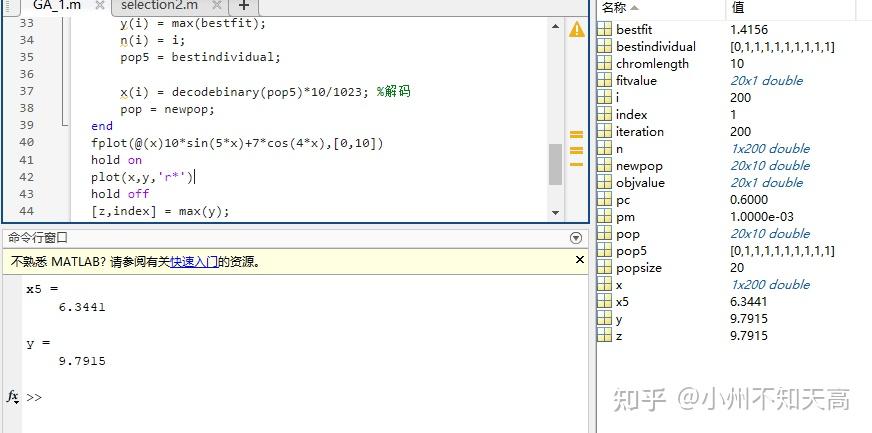
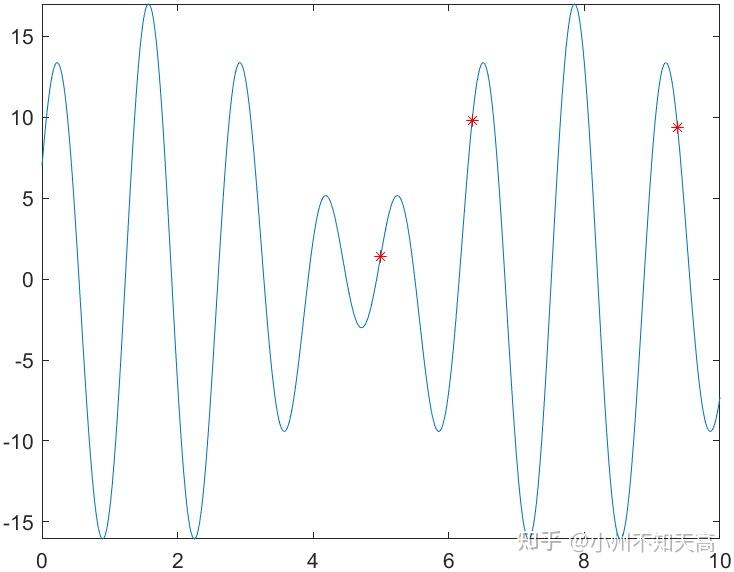
由图能看出来结果并非最好
我们调整iteration->500
来看结果:
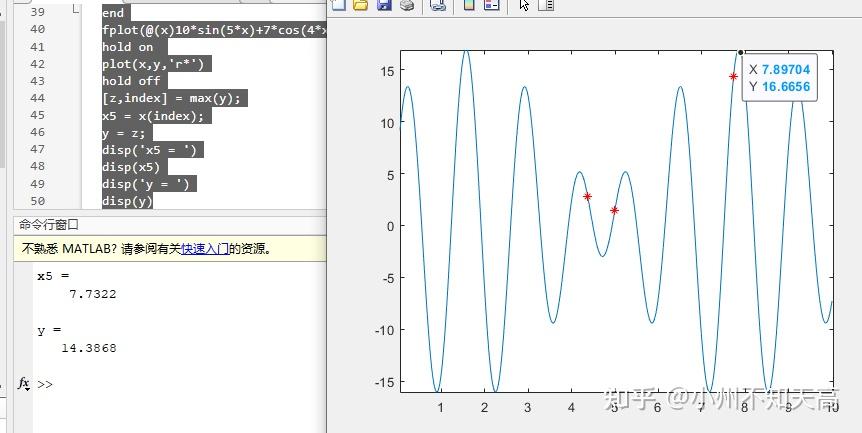
值得一提的是遗传算法因为初始化的种群是随机的,所以同样的程序运行两次,其答案也会略有差异!
这时,我们可以选择多运行几次来寻求较优的解作为我们最后的结果!
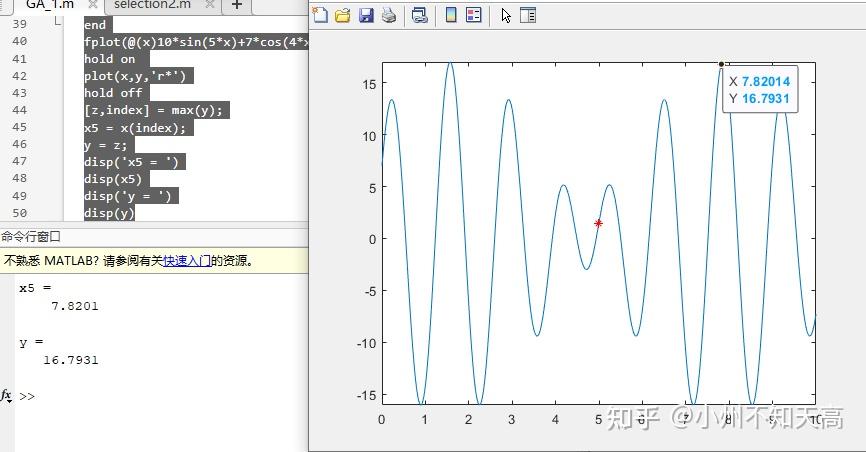
可以看到,这次的结果就相当使人满意,得到满意的数据一定要及时保存好数据!!!
OK!遗传算法就先讲到这里,感兴趣的小伙伴可以拿上免费的源代码去自己试试!
提醒各位,本例是一个及其简单的优化问题,遗传算法能做的远不止如此,后续需要大家更加认真的去拓展!不可懈怠!!!
链接:https://pan.baidu.com/s/1q-zWkgznZJAgaSxaIWaRiQ
提取码:y6gw
文章有谬误之处,敬请各位海涵,并且作者诚恳地希望能够得到指点,不胜感激!!!
地址:海南省海口市58号 电话:0898-88889999 手机:13988888888
Copyright © 2012-2018 首页-速盈娱乐-注册登录站 ICP备案编号:琼ICP备88889999号



 88889999
88889999

